
If you have taken a course on options, it’s likely you have gone through one or multiple derivations of Black-Scholes. Odds are you stared at Ito’s Lemma for a few minutes and wondered why you didn’t instead join your friends in brute forcing into your brain a walk-through of “what happens to the three financial statements when depreciation goes up by $10” 1. But you persevered. You graduated, landed a job in NYC, and moved into an East Village apartment, which, like a Mayan temple, only gets sunlight once a year in the winter solstice.
As a newly-minted trader, structurer, or (God forbid) salesperson, you have to price derivatives - something that likely looks like choosing an underlyer (e.g. the S&P 500 or natural gas futures), a type of derivative contract (e.g. a vanilla call option or a “phoenix autocall”), a maturity (e.g. 1-month or 20Apr2025) and then inputting some numbers.
Very quickly you will realize that, for most simpler derivatives such as vanilla calls or puts, basically only two things matter: the “forward” and the “vol”.
A quick detour on forward pricing
By far, the most useful outline of forward pricing I have seen is in Natenberg2. The main thing is that it completely erases the need to memorize whether “rates have a plus while dividends have a minus” in the formula (i.e. \(F=Se^{(r-d)t}\)), but instead gives you a framework (or mental model) to think about it.
In sum, a forward is nothing more than a handshake in which you agree to purchase something for a given price in the future. This should have some benefits as well as some disadvantages versus purchasing that thing today. So at a very high level:
forward price = current price + (benefits of buying later - benefits of buying now) = current price + (costs of buying now - benefits of buying now)
In the case of a stock trading now at \(S\):
- Option 1: buy stock now, hold it for one year.
- Benefit: earn \(d \times S\) in dividends (assuming \(d\) is dividend yield of stock)
- These dividends are a benefit of buying stock now and a cost of buying later (opportunity cost)
- Option 2: buy “forward” on stock i.e. agree to buy stock for \(F\) in 1 year.
- Benefit: earn \(r \times S\) in interest (you didn’t spend money so you get to invest it)
- This interest is a benefit of buying later and a cost of buying now (opportunity cost)
As a result, the forward should have a price that looks something like: current price + interest earned from not outlaying any cash now - dividends forgone from buying later. You can draw a nice table of cash flows and convince yourself, via no arbitrage, that \(F=Se^{(r-d)t}\).
The nice thing about understanding the framework rather than just remembering the formula is that you should be able to generalize it to new contexts. Let’s say instead of a stock we were talking about barrels of oil: buying now has the disadvantage of, well, having to deal with storing actual barrels of oil. Precisely like the dividends case for stocks, storage cost is a key cost for buying physical commodities now, so you would expect it to show up in the formula following a plus sign - a negative cash flow you forgo by choosing to buy the future.
The set up
One way to think about derivatives pricing roughly involves the following steps3:
- simulate many different trajectories of the underlying asset, from the onset of the contract up to its maturity
- look at the array of terminal values and apply your contract’s payoff function to them
- take the average those payoffs
- bring that payoff to present value
Step 1 is arguably the hardest one: you have to pick a model to describe the behavior of the underlying asset over time, which begs the choice of a process and its parameters.
Let’s simply assume the underlyer is a stock that follows a Geometric Brownian Motion with some reasonable parameter choices (risk-free rate, dividend yield, and volatility). You can expand the shaded section below to see the relevant code along with the prompt used to have GPT o3-mini generate it.
Click to expand and see source prompt and code
Prompt:
can you code some nice looking charts illustrating that if we simulate many different paths for a stock with some dividend yield and assume some interest rate, the forward will be the center of that distribution? generate two plots: on the left, show a subset of the generated paths over time as line plots, making sure to emphasize the forward drift line among the random paths around it. on the right, plot the distribution of terminal values and two vertical lines: one marking the average simulated terminal value and another marking the forward value
GPT o3-mini response (with very minor, if not just aesthetic, changes done by me):
import numpy as np
import matplotlib.pyplot as plt
# Simulation parameters
S0 = 100.0 # Initial stock price
r = 0.05 # Risk-free interest rate (annualized)
q = 0.02 # Dividend yield (annualized)
sigma = 0.2 # Volatility (annualized)
T = 1.0 # Time to maturity (in years)
# -------------------------------
# Part 1: Simulate and Plot Sample Paths
# -------------------------------
# Use daily steps for the path simulation
n_steps = 252 # Number of time steps (e.g., trading days in a year)
dt = T / n_steps
time = np.linspace(0, T, n_steps + 1)
# Number of sample paths to show (for clarity, we use a small number)
n_sample_paths = 1000
sample_paths = np.zeros((n_sample_paths, n_steps + 1))
sample_paths[:, 0] = S0
# Set seed for reproducibility
np.random.seed(42)
# Simulate each sample path using geometric Brownian motion with dividend yield.
# Under the risk-neutral measure, the dynamics are:
# dS/S = (r - q) dt + sigma dW,
# which leads to the discrete solution:
# S(t+dt) = S(t) * exp[(r - q - 0.5*sigma^2)*dt + sigma*sqrt(dt)*Z]
for i in range(n_steps):
Z = np.random.normal(size=n_sample_paths)
sample_paths[:, i + 1] = sample_paths[:, i] * np.exp((r - q - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
# Calculate the forward expected path at any time t:
# E[S(t)] = S0 * exp((r - q)*t)
forward_path = S0 * np.exp((r - q) * time)
# -------------------------------
# Part 2: Simulate Terminal Stock Prices for Histogram
# -------------------------------
# For a more robust histogram, simulate many paths (only terminal values needed)
n_paths_hist = 10000
Z_hist = np.random.normal(size=n_paths_hist)
ST = S0 * np.exp((r - q - 0.5 * sigma**2) * T + sigma * np.sqrt(T) * Z_hist)
simulated_mean = np.mean(ST)
simulated_m1sig = simulated_mean - np.std(ST)
simulated_p1sig = simulated_mean + np.std(ST)
# Calculate the forward price for maturity T:
forward = S0 * np.exp((r - q) * T)
# -------------------------------
# Plotting: Sample Paths and Histogram
# -------------------------------
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
# Plot 1: Sample Paths over Time
for i in range(n_sample_paths):
ax[0].plot(time, sample_paths[i], lw=1, label=f'Simulated Paths' if i < 1 else None, alpha=0.5)
# Plot the forward expected path (risk-neutral expected value)
ax[0].plot(time, forward_path, 'k--', lw=2, label='Forward Expected Path')
ax[0].set_xlabel('Time (years)')
ax[0].set_ylabel('Stock Price')
ax[0].set_title(f'Simulated Stock Paths (only showing {n_sample_paths:,})')
ax[0].legend()
ax[0].grid(True)
# Plot 2: Histogram of Terminal Stock Prices at T
ax[1].hist(ST, bins=50, density=True, alpha=0.6, color='skyblue', edgecolor='black')
ax[1].axvline(simulated_mean, color='blue', linestyle='--', linewidth=2,
label=f'Simulated Avg = {simulated_mean:.2f}')
ax[1].axvline(forward, color='red', linestyle='--', linewidth=2,
label=f'Forward = {forward:.2f}')
ax[1].axvline(simulated_m1sig, color='green', linestyle='--', linewidth=2,
label=f'Simulated Avg - 1stdev = {simulated_m1sig:.2f}')
ax[1].axvline(simulated_p1sig, color='green', linestyle='--', linewidth=2, label=f'Simulated Avg - 1stdev = {simulated_p1sig:.2f}')
ax[1].set_xlabel('Stock Price at Maturity (T)')
ax[1].set_ylabel('Probability Density')
ax[1].set_title(f'Distribution of Terminal Stock Prices ({n_paths_hist:,} paths)')
ax[1].legend()
ax[1].grid(True)
plt.tight_layout()
plt.show()
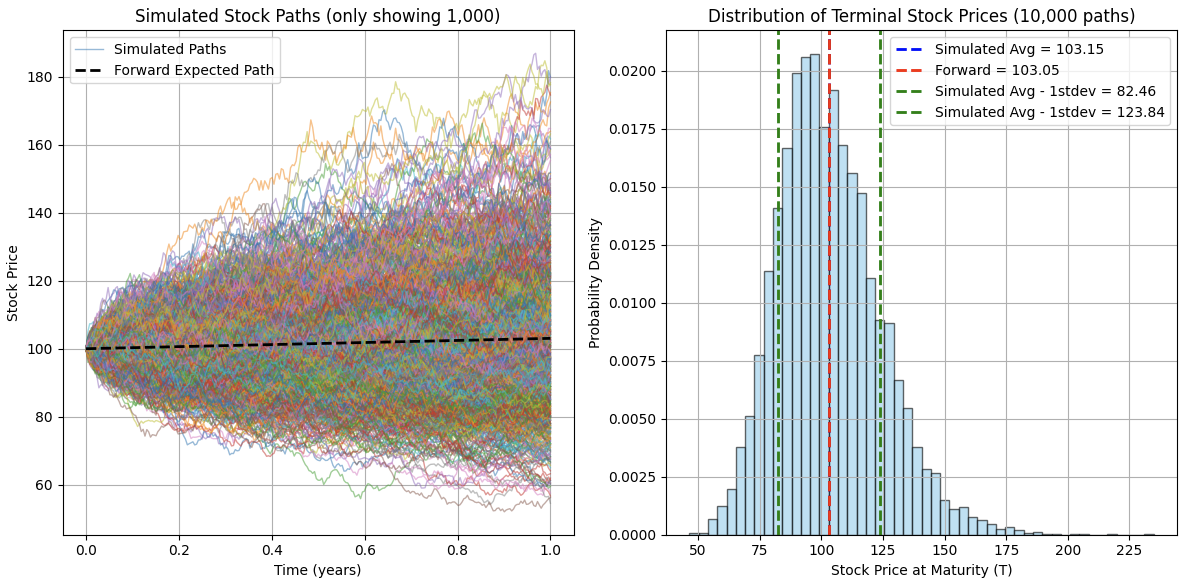
The above charts illustrates steps 1 and 2:
The left plot shows the evolution of a sample of 1,000 simulated paths for our stock for 1 year.
- The dashed black line shows a line which simply accrues daily the “forward rate” given by \(r-d\), the difference between the risk-free rate and the dividend yield (I’ve assume \(r=0.05\) and \(d=0.02\), implying the black line drifts by 3% yearly or 3% / 252 = 0.012% = 1.2bps a day).
More interestingly, the plot on the right shows the distribution of terminal values for 10,000 simulated paths for our stock.
- The dashed red line marks the terminal value for the black path on the left chart: one that simply drifts by the forward rate. As a result, it is not surprising that it ends up very close to 103 (3% return on an assumed 100 initial value).
- The dashed blue line (hard to see as it’s very close to the red one) marks the average terminal value i.e. the mean value of the plotted distribution.
- The dashed green lines mark plus and minus one standard deviation from the mean in this distribution. Also not surprisingly, since we generated 1 year paths, this is not too far from our assumed 20% volatility (1std = 20.69 in this example4)
That’s a lot of information, but understanding this is very powerful and should be the key to figuring out why everything revolves around “forward” and “vol”. I will skip covering volatility to great detail here as I think its place in this framework is relatively easy to grasp: the higher the volatility, the higher the dispersion of paths at maturity. Now, a key question is: what are paths dispersed around?
The forward is the underlyer, not spot
I have glanced over the fact that in the right plot above, the simulated average and the forward value are remarkably close. A reasonable hypothesis is that the terminal value distribution is centered around the forward value.
First, we’ll quickly gather some ammo. Good old Put-Call Parity5 tells us something like “you can create a forward by buying a call and shorting a put, both struck at the forward price”, a so-called “synthetic forward”.
If options were trading in a way that imply a distribution whose mean is different from the forward price, we could get a little bit creative. Let’s say option markets are pricing a distribution with mean above the current forward price: you should be sensing “option package expensive, forward cheap”. Specifically, you should be able to:
- sell the synthetic forward built by going short a call and long a put both struck at the forward price
- buy the actual forward (or equivalently, borrow cash and purchase the asset)
This portfolio yields a risk-less profit at inception because the synthetic forward should fairly be worth \(S_0e^{−dT}−Fe^{−rT}\) (by put–call parity), the mispricing implies an immediate “extra” cash inflow of:
$$Δ=[C(F)−P(F)]−S_0e^{−dT}−Fe^{−rT}>0$$| Cash flow | Leg 1 (short synthetic forward) | Leg 2 (long actual forward) | Total cash flow |
|---|---|---|---|
| Time = 0 | \(\Delta > 0\) (see above for details) | 0 | \(\Delta>0\) |
| Time = Maturity | \(-[S(T)-F]\) | \(S(T)-F\) | 0 |
In words: you are able to structure a trade in which selling the “mispriced” synthetic forward produces some positive cash flow at inception, while the position is risk-less at maturity since the two legs perfectly offset each other.
As a result, in this setting, we can conclude that the terminal value distribution of underlyer has to be centered around the forward, else there would be an abirtrage opportunity.
Taking a step back: typically, we are taught that options are a function of an underlyer such as a stock, or a spot price of an index, etc. And as a consequence, those underlyers come with “baggage”: an interest rate6, dividend yield, etc. This is why a class on derivative usually starts covering exclusively stocks with no dividends, only to then introduce dividends later as an “adjustment” to the baseline Black-Scholes model.
The key shift in perspective is: instead, options are effectively a function of the forward price of the underlyer at the relevant maturity date. Things like interest rates and dividends impact where the forward is relative to spot, but that information is entirely conveyed by \(\frac{F}{S}\).
Worth noting that this is nowhere a new insight and, in fact, is the foundation of a model published by Fischer Black in 1976. You could argue this model is a nice simplification of Black-Scholes, but I’d argue the basic Black-Scholes first taught in school is a simplification of this model, as it generalizes to asset classes in which either the underlyer is by default the forward because spot is not directly tradeable (e.g. VIX) or because it’s a pain to trade spot (e.g. physical commodities).
Click to expand and see code
import numpy as np
import matplotlib.pyplot as plt
# Base parameters
S0 = 100.0 # Initial stock price
sigma = 0.2 # Volatility (annualized)
T = 1.0 # Time to maturity (in years)
n_steps = 252 # Number of time steps (daily steps)
dt = T / n_steps
time = np.linspace(0, T, n_steps + 1)
# Set a seed for reproducibility.
np.random.seed(42)
# Define four different forward drift values (r - q)
fwd_rates = [-0.3, 0.0, 0.3]
# Number of paths for simulation
n_sample_paths = 100 # For sample path plot (kept low for clarity)
n_paths_hist = 10000 # For histogram of terminal prices
# Create a figure with 4 rows and 2 columns.
fig, axs = plt.subplots(len(fwd_rates), 2, figsize=(10, 10), sharex='col', sharey='col')
fig.suptitle("Effect of forward rate on GBM Paths and Terminal Price Distribution", fontsize=12, y=0.925)
for idx, fwd in enumerate(fwd_rates):
# -------------------------------
# Part 1: Simulate and Plot Sample Paths
# -------------------------------
sample_paths = np.zeros((n_sample_paths, n_steps + 1))
sample_paths[:, 0] = S0
# Simulate sample paths using GBM dynamics:
# S(t+dt) = S(t) * exp[( (r - q) - 0.5*sigma^2)*dt + sigma*sqrt(dt)*Z ]
# Here we directly use 'fwd' as (r - q)
for i in range(n_steps):
Z = np.random.normal(size=n_sample_paths)
sample_paths[:, i + 1] = sample_paths[:, i] * np.exp((fwd - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
# Calculate the forward (expected) path: E[S(t)] = S0 * exp((r - q)*t)
forward_path = S0 * np.exp(fwd * time)
ax_path = axs[idx, 0]
# Plot all sample paths (using a light line for clarity)
for path in sample_paths:
ax_path.plot(time, path, lw=1, alpha=0.6)
# Overlay the forward expected path (dashed black line)
ax_path.plot(time, forward_path, 'k--', lw=2, label=f'Forward = {forward_path[-1]:.2f}')
ax_path.set_xlabel("Time (years)", fontsize=8)
ax_path.set_ylabel("Stock Price", fontsize=8)
ax_path.set_title(f"Simulated paths, Forward rate = (r - q) = {fwd:.0%}", fontsize=10)
ax_path.legend()
ax_path.grid(True)
# -------------------------------
# Part 2: Simulate Terminal Stock Prices for Histogram
# -------------------------------
Z_hist = np.random.normal(size=n_paths_hist)
# Terminal stock price at T:
ST = S0 * np.exp((fwd - 0.5 * sigma**2) * T + sigma * np.sqrt(T) * Z_hist)
simulated_mean = np.mean(ST)
simulated_std = np.std(ST)
simulated_m1sig = simulated_mean - simulated_std
simulated_p1sig = simulated_mean + simulated_std
# The theoretical forward price at maturity
forward_T = S0 * np.exp(fwd * T)
ax_hist = axs[idx, 1]
ax_hist.hist(ST, bins=50, density=True, color='skyblue', edgecolor='black', alpha=0.7)
ax_hist.axvline(simulated_mean, color='blue', linestyle='--', linewidth=2,
label=f'Sim Avg = {simulated_mean:.2f}')
ax_hist.axvline(forward_T, color='red', linestyle='--', linewidth=2,
label=f'Forward = {forward_T:.2f}')
ax_hist.axvline(simulated_m1sig, color='green', linestyle='--', linewidth=2,
label='Avg - 1 SD')
ax_hist.axvline(simulated_p1sig, color='green', linestyle='--', linewidth=2,
label='Avg + 1 SD')
ax_hist.set_xlabel("Terminal Stock Price", fontsize=8)
ax_hist.set_ylabel("Probability Density", fontsize=8)
ax_hist.set_title(f"Terminal price distribution, Forward rate = {fwd:.0%}", fontsize=10)
ax_hist.legend()
ax_hist.grid(True)
plt.tight_layout(rect=[0, 0, 1, 0.93])
plt.show()
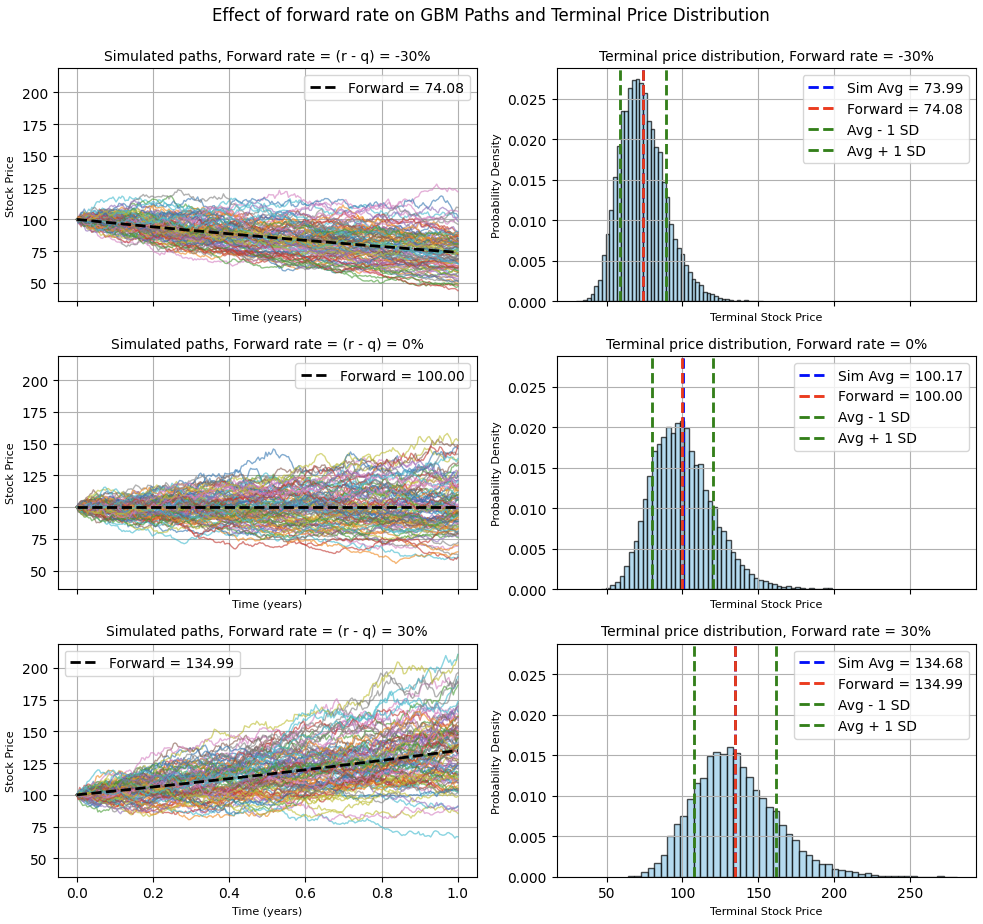
In sum
This was a long way to say that, for vanilla options, there’s a reason why a lot around pricing options revolves around choosing a (forward, vol) pair. These two parameters encompass the main aspects of options pricing7. That is not to say that they encompass everything - far from that - but by simplifying the underlyer dynamics around one key parameter, one can go a long way in thinking about options by focusing on the forward and volatility. This is a much simpler framework than those taught in option courses at schools.
What’s are some practical use cases of this? Well, grossly put, option prices grow with volatility: more vol increases the chances that the option expires in-the-money. Forwards, however, are interesting!
- Call option prices increase with higher forward: the higher the forward, the more the mean expected path of the underlyer will go up. As a result, increasing the forward shifts the terminal value distribution to the right, which makes it more likely that the call expires in-the-money
- Put option prices decrease with higher forward: conversely, if the distribution shifts right, it’s less likely that puts expire in-the-money
This is why options people frequently think in “ATMF” (at-the-money-forward) terms as opposed to ATM (or ATMS, “at-the-money-spot”). It’s a very convenient place to be as the probability to expiring in the money is close to 50%: ~50% of all possible paths will be below the forward, and ~50% of all possible paths will be above it8.
Further, realizing that options really are derivatives of the forward sheds light some challenges around hedging. As the forward price embeds the market implied cost of financing of the spot position (at rate \(r\)) and dividend yield (at rate \(d\)), you have that “locked in”. If either were to change significantly (for example, let’s say stock became hard to borrow or management decided to substantially change their dividends policy), your hedge is quite imperfect. This is one of the reasons some dividend markets are liquid: banks are very keen to offload that risk to adventurous counterparties.
Not only do I hope to have convinced you that options are about the forward not spot, but that thinking in terms of “what happens to the general profile of the paths I’m simulating” when changing a model parameter is an easy hack to sometimes answer tricky questions.
This is likely the case if you, like me, studied economics or finance. If you were a math or CS person, then you probably were benchmarking to your buddies crunching LeetCode. ↩︎
Sheldon Natenberg’s “Option Volatility & Pricing” - Chapter 2 of the 2nd edition. ↩︎
One important caveat that options math nerds will point out is that a lot of what I am throwing around is only true in a “risk-neutral” sense. That is right, but outside of the scope of this post. If you know what “Girsanov theorem” is, then you probably stay until too late in the office trying to explain to your trader why they are bleeding vega on that one book even though vols were “pretty chill today”. ↩︎
You might wonder: 20.7 seems awfully far from our assumed 20% yearly volatility, did I do something wrong? If I have, then I will kindly point out that GPT o3-mini, with its PhD level knowledge, made the mistake. But assuming I haven’t, its worth thinking about what the 20.7 actually means. Hint: I am giving you the arithmetic standard deviation of terminal values, but consider \(S(T)=S_0 e^{(r−d−\frac{1}{2}\sigma^2)T+\sigma \sqrt{T}Z}\), \(Z = N(0,1)\) and \(var[S(T)]= E[S(T)^2] - E[S(T)]^2\). I leave it to the reader to get there (ha! get rekt). ↩︎
There are plenty of great resources on Put-Call parity out there, so I won’t go too deep into it. Like the case for forward pricing, I would encourage you to think about it from a first principles/no arbitrage rather than memorizing the formula - it’s a pretty powerful thing. ↩︎
Let’s set concerns with borrow rates and that kind of stuff aside. ↩︎
In a real world setting, one would likely take “fair” (mid) marks for both the forward and vol and add bumps to them in a way that would produce the relevant desired bid or offer for the option package being priced. ↩︎
It’s not precisely 50% and, as a result, not exactly a 50-delta option, but not particularly important here. ↩︎